Geometrická řada: Matematický nástroj pro modelování růstu a poklesu
Úvod do geometrické řady
Geometrická řada je fascinující matematický koncept, který hraje klíčovou roli v modelování růstu a poklesu v různých oblastech. Tato posloupnost čísel, kde každý následující člen je násobkem předchozího o konstantní faktor, poskytuje elegantní způsob, jak popsat mnohé přírodní a ekonomické jevy. Od finančních prognóz až po populační dynamiku, geometrická řada nabízí mocný nástroj pro pochopení světa kolem nás.
Co je geometrická řada?
Geometrická řada je definována jako posloupnost čísel, kde poměr mezi dvěma po sobě jdoucími členy zůstává konstantní. Tento poměr se nazývá kvocient řady. Matematicky lze geometrickou řadu vyjádřit jako:
a, ar, ar², ar³, …, ar^(n-1)
kde ‚a‘ je první člen řady, ‚r‘ je kvocient a ‚n‘ je počet členů.
Příklady geometrických řad z reálného života zahrnují:
- Růst bakteriální populace, která se každou hodinu zdvojnásobí
- Znehodnocení automobilu, které každý rok klesá o 15%
- Úročení vkladů s fixní úrokovou sazbou
Základní pojmy geometrické řady
Pro plné pochopení geometrické řady je důležité seznámit se s jejími základními pojmy:
- První člen (a): Počáteční hodnota řady.
- Kvocient (r): Konstantní poměr mezi po sobě jdoucími členy.
- n-tý člen: Obecný vzorec pro n-tý člen geometrické řady je: a_n = a * r^(n-1)
kde a_n představuje n-tý člen řady, ‚a‘ je první člen, ‚r‘ je kvocient a ‚n‘ je pořadí členu.
Rozdíl mezi aritmetickou a geometrickou řadou
Pro lepší pochopení specifik geometrické řady je užitečné porovnat ji s aritmetickou řadou:
| Definice | Rozdíl mezi po sobě jdoucími členy je konstantní | Poměr mezi po sobě jdoucími členy je konstantní |
| Obecný člen | a_n = a + (n-1)d | a_n = a * r^(n-1) |
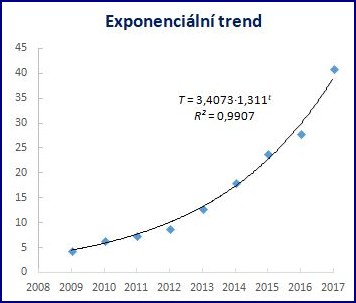
| Růst | Lineární | Exponenciální |
| Příklad | 2, 5, 8, 11, 14, … | 2, 6, 18, 54, 162, … |
| Použití | Lineární procesy | Exponenciální růst/pokles |
Vzorce a výpočty geometrické řady
Pro efektivní práci s geometrickými řadami je nezbytné ovládat klíčové vzorce a postupy výpočtů.
Součet prvních n členů geometrické řady
Vzorec pro součet prvních n členů geometrické řady je:
S_n = a * (1 – r^n) / (1 – r), pro r ≠ 1 S_n = n * a, pro r = 1
kde S_n je součet, ‚a‘ je první člen, ‚r‘ je kvocient a ‚n‘ je počet členů.
Příklad výpočtu: Uvažujme geometrickou řadu s prvním členem a = 3 a kvocientem r = 2. Vypočítejme součet prvních 5 členů.
S_5 = 3 * (1 – 2^5) / (1 – 2) = 3 * (1 – 32) / (-1) = 3 * 31 = 93
Součet nekonečné geometrické řady
Pro nekonečnou geometrickou řadu platí specifické podmínky konvergence a výpočtu součtu.
Kroky pro výpočet součtu nekonečné geometrické řady:
- Ověřte, zda |r| < 1 (absolutní hodnota kvocientu je menší než 1).
- Pokud podmínka platí, řada konverguje a lze použít vzorec: S_∞ = a / (1 – r)
- Pokud |r| ≥ 1, řada diverguje a nemá konečný součet.
- Vypočítejte součet dosazením hodnot do vzorce.
- Interpretujte výsledek v kontextu problému.

Praktické aplikace geometrické řady
Geometrické řady nacházejí uplatnění v mnoha oblastech praxe i vědy.
Finanční matematika
V oblasti financí se geometrické řady využívají například pro výpočet složeného úročení. Uvažujme příklad:
Vklad 1000 Kč s ročním úrokem 5% po dobu 10 let.
Použijeme vzorec: A = P * (1 + r)^n kde A je konečná částka, P je počáteční vklad, r je úroková míra a n je počet let.
A = 1000 * (1 + 0.05)^10 = 1628.89 Kč
Přírodní vědy a technika
Geometrické řady mají široké uplatnění v přírodních vědách a technice:
- Biologie: Modelování růstu populací
- Fyzika: Rozpad radioaktivních látek
- Akustika: Výpočet ozvěny v uzavřených prostorech
- Optika: Výpočet intenzity odraženého světla
- Elektrotechnika: Analýza elektrických obvodů
Řešení úloh s geometrickou řadou
Krokový postup řešení
- Identifikujte první člen (a) a kvocient (r) řady.
- Určete, zda se jedná o konečnou nebo nekonečnou řadu.
- Vyberte vhodný vzorec podle typu úlohy.
- Dosadťe známé hodnoty do vzorce.
- Proveďte výpočet a zkontrolujte výsledek.
- Interpretujte řešení v kontextu zadání.
Časté chyby a jak se jim vyhnout
- Záměna vzorců pro aritmetickou a geometrickou řadu
- Nesprávné určení kvocientu
- Opomenutí kontroly konvergence u nekonečných řad
- Chybná interpretace výsledků v kontextu reálného světa
Tipy pro správné řešení:
- Pečlivě analyzujte zadání úlohy
- Ověřte, zda se opravdu jedná o geometrickou řadu
- Vždy zkontrolujte podmínky použití vzorců
- Proveďte zpětnou kontrolu dosazením výsledku
Geometrická řada v moderní matematice
Zobecněné geometrické řady
Moderní matematika rozšiřuje koncept geometrických řad o složitější struktury:
- Geometrické řady s proměnným kvocientem
- Multidimensionální geometrické řady
- Geometrické řady v komplexní rovině
Tyto zobecnění umožňují modelovat složitější systémy a procesy v různých vědeckých disciplínách.
Aplikace v teorii pravděpodobnosti
Geometrické řady hrají významnou roli v teorii pravděpodobnosti, zejména při modelování:
- Pravděpodobnosti úspěchu v opakovaných nezávislých pokusech
- Času do prvního úspěchu v Bernoulliho procesech
- Očekávané hodnoty geometricky distribuovaných náhodných veličin
Tyto aplikace jsou klíčové pro analýzu rizik, teorii her a stochastické modelování.
Závěr
Geometrická řada představuje mocný matematický nástroj s širokým spektrem aplikací. Od základních finančních výpočtů po pokročilé vědecké modely, její význam v matematice a reálném světě je nepopiratelný. Pochopení principů geometrické řady otevírá dveře k hlubšímu porozumění mnoha přírodním a ekonomickým jevům. Pro studenty a profesionály v oblasti matematiky, přírodních věd a financí je ovládnutí konceptu geometrické řady klíčovým krokem k rozvoji analytických schopností a kritického myšlení. Další studium tohoto fascinujícího tématu může vést k objevení nových souvislostí a aplikací, které mohou přispět k řešení komplexních problémů současného světa.
